Загальне
Орловський І.В., Тимошенко О.А.
Національний технічний університет України “Київський політехнічний інститут імені Ігоря Сікорського”, Київ, Україна
Особливості побудови покрокових тестів у системі Moodle та досвід їх впровадження в навчальний процес
Характерною тенденцією останніх років є активне використання при навчанні новітніх інформаційних технологій. Системи тестового контролю є важливим елементом освітнього процесу та є складовою багатьох освітніх проектів МОН України, тому особливого значення набуває комп'ютерне тестування, як засіб контролю за рівнем засвоєння знань студентами у ЗВО. Проведення електронних контрольних та іспитів у вищій школі стають все більш актуальними та важливими. На кафедрі математичного аналізу та теорії ймовірностей Національного Технічного Університету України «Київського політехнічного інституту імені Ігоря Сікорського» існує багаторічний досвід роботи з тестами для математичних дисциплін, які викладаються для різних спеціальностей університету [1-3].
Найбільш поширеними серед існуючих пакетів тестів для математичних дисциплін є тести відкритого та закритого типів. Однак, перераховані тести не дають можливості перевірити всі логічні кроки розв'язання задачі та записати розгорнуту відповідь. Вони дають можливість перевірити або тільки відповіді або деякий проміжний крок.
Саме тому, викладачами кафедри математичного аналізу та теорії ймовірностей було розпочато розробку так званих «покрокових тестів» (див. Рис. 1), які представляють собою послідовність тестових завдань відкритого та закритого типів, об'єднаних в одне завдання з метою перевірки ходу розв'язання та остаточної відповіді певної задачі [4]. Структурно завдання такого типу мають складатись із перевірки основних етапів розв'язання (Приклад завдання, зображеного на Рис. 1 див. тут).
Покрокові тести було розроблено з застосуванням відкритої освітньої системи управління навчанням Moodle із застосуванням мови розмітки веб-сторінок HTML. Головною складністю створення подібних тестів є індивідуальний підхід до кожного задання, який вимагає окрім правильної постановки задачі, побудову такого алгоритму розв’язання задачі, який ураховував би можливості інструментарію обраної платформи Moodle по створенню тестів.
Завдання. Знайти вказані мінор та алгебраїчне доповнення

Рис.1. Приклад вигляду завдання покрокового тесту в системі Moodle із застосуванням HTML коду.
Перші покрокові тести в КПІ ім. Ігоря Сікорського було розроблено колективом авторів кафедри математичного аналізу та теорії ймовірностей для теми «Елементи лінійної алгебри» кредитного модулю «Лінійна алгебра та аналітична геометрія», які були успішно апробовані на різних факультетах. У тестуванні прийняли участь 97 студентів першого курсу у 2017\2018 н.р. та 297 студентів у 2018\2019 н.р. Було проведено аналіз покрокових тестів [5-6] та виявлено наступні переваги:
- можливість заміни традиційних розрахункових робіт, що дозволить з меншими навантаженнями на викладача, який витрачає багато часу і зусиль на перевірку великої кількості одноманітних завдань;
- можливість автоматизованого написання, контрольних робіт та складання іспиту у формі максимально наближеній до аналогічних видів традиційного письмового контролю;
- тести вимагають покрокового розв'язання завдань, вгадування відповіді не є можливим;
- коректно складені покрокові тести із структурою, побудованою за лінійним алгоритмом мають високу надійність, узгодженість між своїми складовими та високу розрізняльну здатність.
- виключення людського фактору, що збільшує об’єктивність оцінювання;
- можливість одразу після написання, або завершення написання групою, побачити оцінку і допущені помилки, що робить більш ефективним зворотній зв’язок.
Але слід зазначити, що повністю виключати, такі традиційні засоби перевірки, як письмові контрольні, залікові та екзаменаційні роботи не бажано, бо покрокові тести мають лінійний алгоритм реалізації, що не дає можливості студенту самому обирати спосіб розв'язання та проявити набуті навички у повній мірі.
Розробка покрокових тестів є достатньо складною, оскільки потребує індивідуального підходу до кожної задачі та приведення розв'язку під лінійний алгоритм, який можна запрограмувати.
Розглянемо детальніше особливості побудови тестового завдання «покрокового типу» на наступному прикладі (Див. Рис.2)
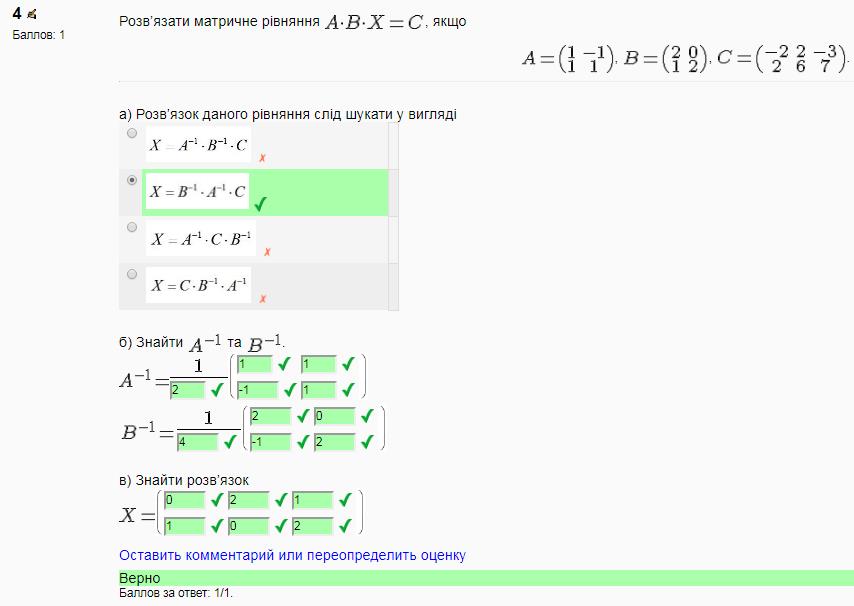
Рис.2. «Покрокове» тестове завдання на знаходження розв'язку матричного рівняння.
Розв'язок такого завдання складається з подолання 3-х кроків.
Крок І. З чотирьох варіантів студент має обрати правильну структуру розв'язку матричного рівняння. Запропоновані варіанти аналогічні та схожі між собою, для того щоб одночасно і заплутати студента і побачити його логіку та знання.
Крок ІІ. На цьому кроці студент має знайти матрицю \(A^{-1}\), яка є оберненою до основної матриці \(A\) та матрицю \(B^{-1}\), яка є оберненою до \(B\). Для цього необхідно знайти визначники цих матриць та всі елементи приєднаних матриць.
Крок ІІІ. Враховуючи результати попередніх кроків студент має перемножити матриці у вибраному порядку та записати розв'язок матричного рівняння.
Отже, на запропонованій моделі було продемонстровано алгоритм перевірки не лише відповіді, а й проміжних етапів розв'язання. Очевидно, що тести покрокового типу є цінними не лише для викладачів, а й для студентів. Останні можуть використовувати тести в якості особистого віртуального репетитора, за допомогою якого можна самостійно розібратися з відповідними темами курсу. Важливо, що студент може відразу після проходження тесту проаналізувати свої помилки, що значно покращує навички в розв'язанні задач відповідного типу і сприяє засвоєнню матеріалу.
Список використаних джерел
- Алєксєєва І. В. Застосування математичних моделей тестів у комплекті дистанційної освіти «Вища математика» / І.В. Алєксєєва, В.О. Гайдей, О.О. Диховичний, Н.Р. Коновалова, Л.Б. Федорова // Математичні машини та системи. – 2010. – №4. – С. 89 – 98.
- Алєксєєва І.В. Про досвід застосування тестових контрольних робіт з вищої математики / І.В. Алєксєєва, В.О. Гайдей, О.О. Диховичний, Н.Р. Коновалова, Л.Б. Федорова // Міжнародна науково-практична конференція «Математика в сучасному технічному університеті», 19—20 квітня 2013 р., Київ: Матеріали конф. — Київ: НТУУ «КПІ», 2013. — С. 442—445.
- Алєксєєва І.В. Про розробку тестових контрольних робіт з курсу «Методи математичної економіки» / І.В. Алєксєєва // Дистанційна всеукраїнська наукова конференція «Математика у технічному університеті XXI сторіччя»,15 – 16 травня 2017р., Краматорськ: Матеріали конф. – Краматорськ, 2017. – С. 284 – 287.
- Алєксєєва І.В. Покрокові тести з курсу «Методи математичної економіки» / І.В. Алєксєєва, І.В. Орловський, Ю.В. Сорокіна // Вісімнадцята міжнародна наукова конференція ім. акад. Михайла Кравчука.-7-10 жовтня,2017.-Луцьк-Київ.-т.2.- С.168-170
- Орловський І. В. Аналіз якості нових методів контролю знань з вищої математики в технічному університеті / І.В. Орловський, О.А. Тимошенко // Шоста міжнародна науково-практична конференція «Математика в сучасному технічному університеті» 28—29 грудня, 2017.- Київ - С. 373-376.
- Омельчук Т. С. Особливості створення та аналіз якості покрокових тестів з лінійної алгебри та аналітичної геометрії / Т.С. Омельчук, І.В. Орловський, О.А. Тимошенко // Сьома міжнародна науково-практична конференція «Математика в сучасному технічному університеті» 27—28 грудня, 2018.- Київ - С. 268-271.